Commas

One of the beautiful qualities of the lattice is that the patterns repeat everywhere. Notes that are in the same relationship to each other on the lattice will always have the same difference in pitch, no matter how where you go. For example, a move of one space to the right will always be a move up a perfect fifth, or 702 cents, wherever it happens.

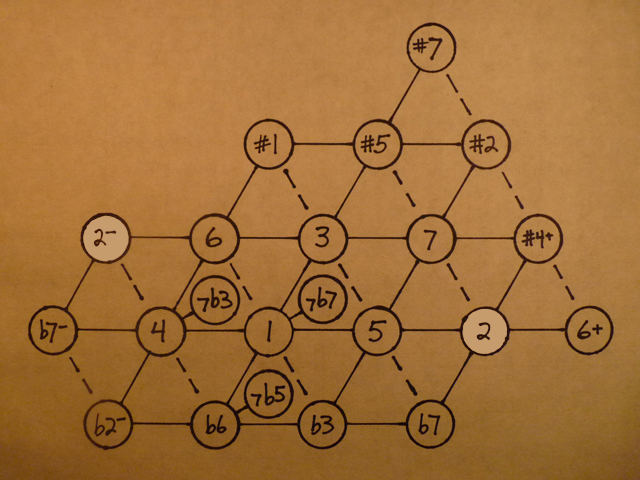The pitch difference between the 2 and 2-, shown in the last post, is about 22 cents (actually 21.5). This is not a big enough difference to be a different scale degree. In the key of C, the 2 is a D. The 2- is also a D, but of a slightly different flavor.

No matter where you are on the lattice, dividing by 5, then multiplying by 3 four times (the distance between the 2- and 2) will result in a pitch difference of 22 cents. The ratio, octave reduced, is 81/80. This sort of small interval is called a comma.

Commas in general are little intervals that pop up again and again in just intonation. There are three or four of them that are important enough to have names. This one is called the syntonic comma, or comma of Didymus, or just plain “comma.” It has its own (very good, I think) Wikipedia article.

There are three such pairs in my home territory of the lattice, the part I currently feel comfortable roaming:

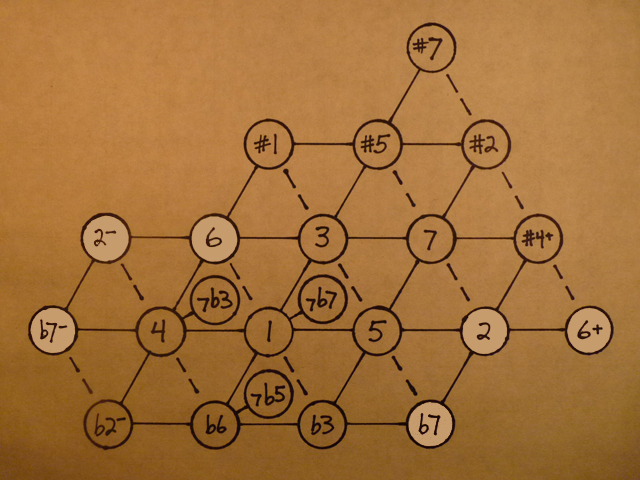Each of the notes in the lower right portion is 22 cents sharp of its namesake in the upper left.

Mathieu calls these pairs of notes Didymic pairs, or comma siblings.

In my naming system, I use a minus sign to show that the note is a Didymic comma flat of its sibling, and a plus sign to show that it’s a Didymic comma sharp.

These siblings start to show how the lattice repeats (almost) as it expands. The almost-duplication goes out forever in all directions.

Next: Another Comma